Memecah Angka, Membangun Pemahaman: Kumpulan Soal Uraian Matematika Kelas 4 tentang Pecahan

Pecahan adalah salah satu konsep fundamental dalam matematika yang sering kali menjadi jembatan penting menuju pemahaman topik-topik yang lebih kompleks di jenjang pendidikan selanjutnya. Bagi siswa kelas 4 Sekolah Dasar, penguasaan konsep pecahan bukan hanya sekadar menghafal definisi, tetapi lebih pada kemampuan mengaplikasikannya dalam berbagai situasi dan memecahkan masalah. Soal uraian menjadi alat yang sangat efektif untuk mengukur kedalaman pemahaman ini, karena memaksa siswa untuk tidak hanya memberikan jawaban, tetapi juga menjelaskan proses berpikir mereka.

Artikel ini akan menyajikan kumpulan soal uraian matematika kelas 4 yang berfokus pada konsep pecahan. Soal-soal ini dirancang untuk menguji berbagai aspek pemahaman, mulai dari pengenalan pecahan, membandingkan, menjumlahkan, mengurangkan, hingga mengaplikasikan pecahan dalam konteks cerita. Dengan menjawab soal-soal uraian ini, diharapkan siswa dapat memperdalam pemahaman mereka, melatih kemampuan berpikir logis, dan membangun kepercayaan diri dalam menghadapi soal-soal matematika.

Mengapa Soal Uraian Penting untuk Pecahan?

Soal uraian (atau esai) menuntut siswa untuk lebih dari sekadar memilih jawaban dari pilihan ganda. Mereka harus:

1. Menjelaskan Konsep: Siswa perlu mampu mengartikulasikan apa arti sebuah pecahan, bagian apa yang diwakilinya, dan bagaimana hubungannya dengan keseluruhan.
2. Memecahkan Masalah Langkah demi Langkah: Soal uraian sering kali melibatkan masalah cerita yang memerlukan pemecahan bertahap. Siswa harus menunjukkan setiap langkah perhitungan dan memberikan alasan di baliknya.
3. Menggunakan Bahasa Matematika: Siswa dilatih untuk menggunakan istilah-istilah matematika yang tepat dalam penjelasan mereka.
4. Menunjukkan Penalaran: Kemampuan untuk menjelaskan mengapa suatu metode dipilih atau mengapa suatu jawaban benar adalah inti dari soal uraian.

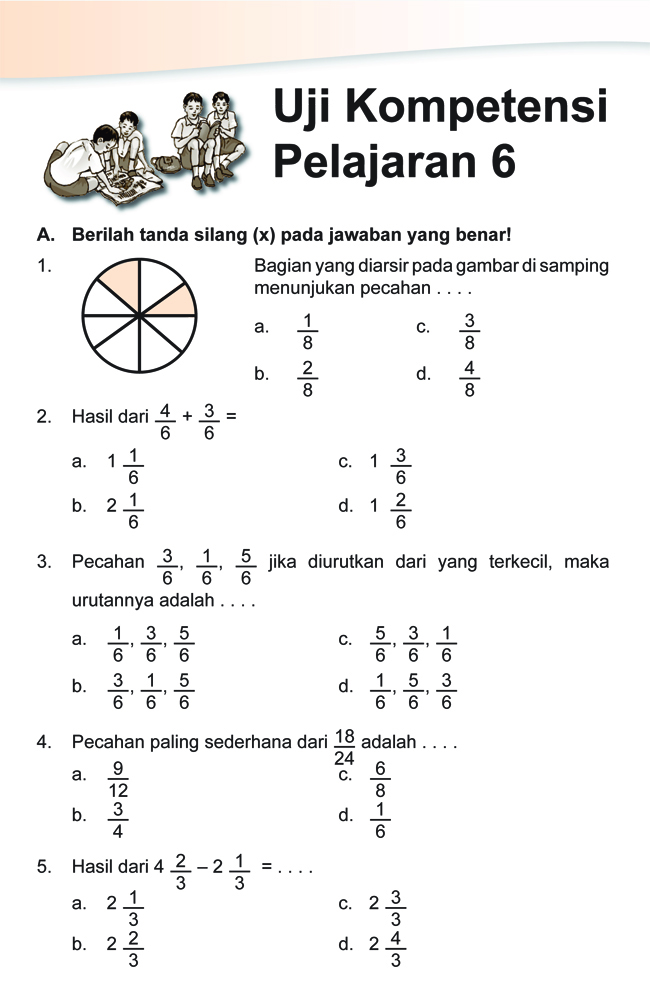
Kumpulan Soal Uraian Matematika Kelas 4 tentang Pecahan

Berikut adalah beberapa contoh soal uraian yang dapat digunakan untuk melatih siswa kelas 4 dalam memahami pecahan. Soal-soal ini dikategorikan berdasarkan tingkat kompleksitas dan konsep yang diuji.

Kategori 1: Pengenalan dan Representasi Pecahan

Pada kategori ini, fokusnya adalah pada pemahaman dasar tentang apa itu pecahan, bagaimana merepresentasikannya, dan mengenali bagian-bagiannya.

1. Soal: Ibu membeli sebuah kue cokelat dan memotongnya menjadi 8 bagian sama besar. Ayah makan 2 potong kue, dan adik makan 3 potong kue.
   a. Berapakah bagian kue yang dimakan Ayah? Jelaskan jawabanmu menggunakan konsep pecahan.
   b. Berapakah bagian kue yang dimakan Adik? Jelaskan jawabanmu menggunakan konsep pecahan.
   c. Jika Ayah dan Adik makan bersama, berapakah total bagian kue yang mereka makan? Tuliskan dalam bentuk pecahan dan jelaskan mengapa demikian.

   • Tujuan: Menguji kemampuan siswa dalam mengidentifikasi pembilang (bagian yang diambil) dan penyebut (total bagian) dari sebuah pecahan dalam konteks benda nyata. Juga melatih penjumlahan pecahan sederhana dengan penyebut yang sama.

2. Soal: Gambarlah sebuah lingkaran. Kemudian, arsir 3/5 bagian dari lingkaran tersebut. Jelaskan mengapa bagian yang kamu arsir mewakili pecahan 3/5.

   • Tujuan: Menguji kemampuan representasi visual pecahan dan kemampuan menjelaskan hubungan antara representasi visual dan notasi pecahan.

3. Soal: Pak Budi memiliki sebuah kebun sayur yang luasnya 10 petak. Dia menanami 4 petak dengan bayam, 3 petak dengan kangkung, dan sisanya ditanami wortel.
   a. Berapakah bagian dari kebun Pak Budi yang ditanami bayam? Tuliskan dalam bentuk pecahan.
   b. Berapakah bagian dari kebun Pak Budi yang ditanami kangkung? Tuliskan dalam bentuk pecahan.
   c. Berapakah bagian dari kebun Pak Budi yang ditanami wortel? Jelaskan langkah-langkahmu untuk menemukan jawabannya.

   • Tujuan: Melatih siswa dalam mengidentifikasi pecahan dari keseluruhan, serta menerapkan konsep pengurangan untuk menemukan bagian yang tersisa.

Kategori 2: Membandingkan Pecahan

Membandingkan pecahan adalah keterampilan penting yang membantu siswa memahami besaran relatif dari bagian-bagian.

4. Soal: Ani memiliki pita sepanjang 1/2 meter, sedangkan Budi memiliki pita sepanjang 1/4 meter. Siapakah yang memiliki pita lebih panjang? Jelaskan alasanmu.

   • Tujuan: Menguji kemampuan siswa dalam membandingkan dua pecahan sederhana dengan penyebut yang berbeda, dengan fokus pada pemahaman konsep "lebih besar" atau "lebih kecil".

5. Soal: Di sebuah pesta ulang tahun, ada dua loyang pizza. Loyang A dipotong menjadi 6 bagian sama besar, dan 3 bagian sudah dimakan. Loyang B dipotong menjadi 8 bagian sama besar, dan 4 bagian sudah dimakan. Loyang mana yang tersisa lebih banyak? Jelaskan cara kamu mengetahuinya.

   • Tujuan: Melatih siswa dalam membandingkan dua pecahan yang berbeda penyebut dan pembilang, serta mengaplikasikan konsep perbandingan dalam situasi nyata. Siswa mungkin perlu menyederhanakan atau mencari penyebut bersama (meskipun penyederhanaan mungkin lebih umum di kelas 4).

6. Soal: Urutkan pecahan berikut dari yang terkecil hingga terbesar: 2/3, 1/3, 3/3, 0/3. Jelaskan alasanmu dalam mengurutkan pecahan-pecahan tersebut.

   • Tujuan: Menguji pemahaman siswa tentang pecahan senilai (dengan penyebut sama) dan pecahan yang mewakili keseluruhan atau ketiadaan.

Kategori 3: Operasi Penjumlahan dan Pengurangan Pecahan

Kategori ini berfokus pada kemampuan siswa melakukan operasi dasar pada pecahan, baik dengan penyebut yang sama maupun yang berbeda (untuk kasus sederhana).

7. Soal: Ayah menggunakan 1/4 liter cat merah dan 2/4 liter cat biru untuk mengecat pagar rumah. Berapa total liter cat yang digunakan Ayah? Tuliskan dalam bentuk pecahan dan jelaskan perhitunganmu.

   • Tujuan: Menguji kemampuan penjumlahan pecahan dengan penyebut yang sama.

8. Soal: Sarah memiliki selembar kertas yang terbagi menjadi 10 bagian sama besar. Dia menggunakan 3/10 bagian kertas untuk membuat origami dan 4/10 bagian untuk menggambar.
   a. Berapa total bagian kertas yang digunakan Sarah? Jelaskan perhitunganmu.
   b. Berapa bagian kertas yang tersisa? Jelaskan perhitunganmu.

   • Tujuan: Melatih penjumlahan dan pengurangan pecahan dengan penyebut yang sama dalam konteks masalah cerita.

9. Soal: Pak Tani memiliki 5/7 hektar sawah. Dia menanami 2/7 hektar dengan padi dan sisanya dengan jagung. Berapa hektar sawah yang ditanami jagung? Jelaskan langkah-langkahmu.

   • Tujuan: Menguji kemampuan pengurangan pecahan dengan penyebut yang sama.

10. Soal: Ibu membuat jus apel. Dia menggunakan 1/3 dari apel yang tersedia untuk membuat jus. Kemudian, dia menggunakan 1/6 dari apel yang tersedia untuk membuat saus apel. Berapa total bagian apel yang digunakan Ibu? Jelaskan cara kamu mencari penyebut yang sama untuk menjumlahkan pecahan tersebut. (Catatan: Soal ini bisa menjadi tantangan lebih untuk siswa yang sudah diajarkan konsep penyebut bersama sederhana).

    • Tujuan: Menguji pemahaman awal tentang penjumlahan pecahan dengan penyebut berbeda, yang memerlukan pencarian penyebut bersama. Untuk kelas 4, fokusnya mungkin pada penyebut yang kelipatannya mudah ditemukan.

Kategori 4: Pecahan dalam Konteks Masalah Cerita yang Lebih Kompleks

Pada bagian ini, soal-soal mengintegrasikan beberapa konsep pecahan atau memerlukan pemikiran yang lebih mendalam untuk menyelesaikannya.

11. Soal: Sebuah botol berisi air. Jika diminum 1/5 bagian, sisanya adalah 4/5 bagian. Jika diminum 2/5 bagian, berapakah bagian air yang tersisa? Jelaskan perhitunganmu.

    • Tujuan: Menguji pemahaman hubungan antara bagian yang diminum dan bagian yang tersisa, serta kemampuan pengurangan pecahan.

12. Soal: Dinda membagi sekotak pensil warnanya. 1/4 bagian diberikan kepada adiknya, dan 1/2 bagian diberikan kepada temannya.
    a. Berapakah total bagian pensil warna yang diberikan Dinda kepada adiknya dan temannya? Jelaskan perhitunganmu.
    b. Berapakah bagian pensil warna yang masih dimiliki Dinda? Jelaskan perhitunganmu.

    • Tujuan: Melatih penjumlahan dan pengurangan pecahan dengan penyebut berbeda (1/4 dan 1/2). Siswa perlu menemukan bahwa 1/2 sama dengan 2/4.

13. Soal: Ada sebuah resep kue yang membutuhkan 3/4 cangkir tepung. Jika Ibu hanya memiliki 1/2 cangkir tepung, berapakah kekurangan tepung yang dibutuhkan Ibu? Jelaskan cara kamu menghitungnya.

    • Tujuan: Menguji kemampuan pengurangan pecahan dengan penyebut berbeda.

14. Soal: Dua teman, Rio dan Sinta, berlomba lari. Rio telah menempuh 3/5 jarak lintasan, sedangkan Sinta telah menempuh 7/10 jarak lintasan. Siapakah yang lebih dekat ke garis finis? Jelaskan alasanmu dengan membandingkan kedua pecahan tersebut.

    • Tujuan: Menguji kemampuan membandingkan pecahan dengan penyebut berbeda dan mengaplikasikannya dalam konteks jarak.

15. Soal: Sebuah pipa air memiliki panjang tertentu. Jika 2/3 bagian dari pipa itu digunakan untuk mengalirkan air ke rumah A, dan 1/6 bagian digunakan untuk mengalirkan air ke rumah B, berapakah total bagian pipa yang digunakan untuk mengalirkan air ke kedua rumah tersebut? Jelaskan cara kamu menyelesaikan masalah ini.

    • Tujuan: Melatih penjumlahan pecahan dengan penyebut berbeda yang memerlukan pencarian penyebut bersama.

Tips untuk Siswa dalam Menjawab Soal Uraian Pecahan

• Baca Soal dengan Seksama: Pahami apa yang diminta oleh soal. Identifikasi informasi penting yang diberikan.
• Gunakan Gambar atau Diagram (Jika Perlu): Visualisasi dapat sangat membantu dalam memahami konsep pecahan. Menggambar lingkaran, persegi panjang, atau garis bilangan bisa menjadi alat bantu yang efektif.
• Jelaskan Setiap Langkah: Jangan hanya menuliskan jawaban akhir. Uraikan setiap langkah perhitungan yang kamu lakukan. Misalnya, "Pertama, saya akan menjumlahkan bagian yang dimakan Ayah dan Adik…"
• Gunakan Bahasa Matematika yang Tepat: Gunakan istilah seperti "pembilang," "penyebut," "keseluruhan," "bagian," "lebih besar dari," "lebih kecil dari," dll.
• Tuliskan Jawaban dalam Kalimat yang Jelas: Setelah melakukan perhitungan, jelaskan arti dari jawaban tersebut dalam konteks soal. Misalnya, "Jadi, total bagian kue yang dimakan Ayah dan Adik adalah 5/8 bagian."
• Periksa Kembali Pekerjaanmu: Pastikan perhitunganmu benar dan penjelasanmu logis serta mudah dipahami.

Kesimpulan

Soal uraian memainkan peran krusial dalam membangun pemahaman yang mendalam tentang konsep pecahan bagi siswa kelas 4. Dengan mendorong mereka untuk menjelaskan proses berpikir, menggunakan bahasa matematika, dan mengaplikasikan konsep dalam berbagai skenario, kita membantu mereka tidak hanya menghafal aturan, tetapi benar-benar memahami mengapa dan bagaimana pecahan bekerja. Kumpulan soal yang disajikan di atas mencakup berbagai aspek penting dari pecahan, mulai dari representasi dasar hingga operasi dan pemecahan masalah cerita. Dengan latihan yang konsisten dan bimbingan yang tepat, siswa kelas 4 akan semakin mahir dalam memecah angka dan membangun pemahaman yang kokoh tentang dunia pecahan.